Encyclopedia of observations
This page is meant to collect the many factual observations and studies people have made about the ciphers over the years. It is a work in progress.
Contents
Z408
Ngram observations
- Cipher contains 62 repeated bigrams (illustration), 11 repeated trigrams (illustration), and 2 repeated quadgrams (illustration).
- In a test of 1,000,000 random shuffles, none had 62 or more repeated bigrams (Plot of distribution), and the average number of repeats was 27.
- In a test of 1,000,000 random shuffles, none had 11 or more repeated trigrams (Plot of distribution), and the average number of repeats was 0.5.
- In a test of 1,000,000 random shuffles, 249 (0.025%) had 2 or more repeated quadgrams (Plot of distribution), and the average number of repeats was 0.0095.
- 5-gram repeating fragments study
- TODO: Multidirectional ngram study (including multiple distances, and repeating fragments)
- TODO: Periodicity of repeating fragments study
- Reading the cipher text from left to right and top to bottom, the longest sequence containing no repeated bigrams starts at position 182, and has length 100 (Illustration)
- Z408 has more period 2 bigrams than expected, while Z340 has fewer than expected (Source: Jarlve)
Unigrams
- Index of Coincidence (IoC) of the cipher is 0.0185. This is 4.6% smaller than the IoC of Z340.
- IoC divided by cipher length (408) is 0.00004534. This is 21% smaller than the IoC per length value for Z340 (Source: Jarlve)
- Some symbols are unusually clustered or unusually spread apart.
- Compared to shuffles, Z408 has fewer than expected outliers of unusually distributed symbols.
Repeated symbols by columns and rows
- The 408 cipher has 6 rows that each contain no repeated symbols (Illustration. Rows are marked in yellow.) In 1,000,000 shuffles, 0.23% of shuffled ciphers had at least 6 rows with no repeated symbols (plot of distribution) (raw data)
- Every column contains at least one repeated symbol.
Homophone cycles
- Several homophone cycles show improved regularity when transcription errors are corrected in the ciphertext (see below)
- The homophone cycle sequence for plaintext letter "L" is not as regular as cycle sequences for other common letters (i.e., his symbols assignments for plaintext "L" were more random) (More details on cycles) The Hardens said they guessed Zodiac would have used the word KILL repeatedly, and an enciphered bigram representing LL occurs 6 times in the cipher text. Perhaps a more regular cycle for L, involving more symbols, would have thwarted this guess by the Hardens.
- Many of the highly regular homophone cycles break down in Part 3 of the cipher text for some unknown reason (More details)
- Tests of cycle significance with shuffle experiments
- Largo's analysis of regularity of homophone cycles
- Longest-repeating substring search for cycles, compared to shuffles
- When comparing all possible ways that length 6 cycles involving 2 symbols can appear, Z408 and Z340 seem to show very similar behavior. (source: Jarlve)
- Evidence of increasingly random cycles in Z408 and Z340 (source: Jarlve)
- Decreasingly random cycles, for both Z408 and Z340, peak when the cipher is shifted 11 rows downwards (source: Jarlve)
Other observations
- The last 18 letters of the 408 decode to a sequence of gibberish: EBEORIETEMETHHPITI
- Many symbols among the last 18 symbols are found directly above in the same columns. The "QEHM" sequence is particularly noteworthy. (Image) (Source: glurk)
- In both Part 1 and Part 3 of the cipher, the QEHM sequence occurs in the exact same location. (Source: DerekP)
- Cragle's observations
- There are misspelled words in the plaintext when the Harden key is applied. When some words are corrected, the symbols assigned to the corrected plaintext letters often resemble the symbols assigned to the original erroneous plaintext letter. (Image). Several homophone cycles show improved regularity when these corrections are made (More details)
- Several symbol/letter assignments in the 408 key seem to reflect adjacencies on QWERTY-layout keyboards (the standard keyboard layout for typewriters and computer keyboards). (Source)
- Statistical tests by _pi and Finder, summarized by Jarlve
- Some plaintext appears to be missing directly in the boundary between Parts 2 and 3 of the cipher ("ALL THE ???? I HAVE KILLED WILL BECOME MY SLAVES") (Annotated plaintext)
- More details on errors in the cipher text and on the Hardens' key
- The "Concerned Citizen" key, sent to Sgt. Lynch of Vallejo PD 2 days after the Hardens' solution was published, contained some differences from the Hardens' key (More details)
- "All roads lead to E" phenomenon of the key (Explanations and details) (Image 1) (Image 2)
- Adjacent sequences in the 408's key (More info)
- Some symbols in the 408 were not reused in the 340's alphabet (Image)
- Zodiac made three statements about the cipher's parts:
- Vallejo times: Here is a cyipher or that is part of one. The other 2 parts have been mailed to the S.F. Examiner + S.F. Chronicle.
- SF Examiner: Here is a cipher or that is part of one. The other 2 parts are being mailed to the Vallejo Times + S.F. Chronicle.
- SF Chronicle: Here is a part of a cipher the other 2 parts of the cipher are being mailed to the editors of the Vallejo Times + SF Examiner.
- Speculation: The following interpretation of the above statements suggests how the parts should be ordered: "Vallejo Times is listed first twice and is the first part. SF Examiner is listed first once and is the second part. SF Chronicle is listed last twice and is the third part." (Source: Jarlve)
- The plaintext solution has a shorter average word length than regular English (4 vs 5) (Source: Jarlve and beijinghouse)
- Comparison of Z408 key with Z340 key via shifts (Source: upsampled)
- Of the three letters sent to newspapers, only the Chronicle's letter said "In this cipher is my identity". This could be interpreted as referring specifically to the cipher portion the Chronicle received, which is the end portion of the cipher which also contains the unsolved 18 characters at the end. Perhaps Zodiac is implying his identity or name can be derived from this portion or the last 18 characters. (Source: Nicodemus)
Kasiski Examination
- A Kasiski examination performed on unigrams in Z408 reveals a spike of 18 repeats at shift of 49
- Among 1,000,000 random shuffles, only 2.2% of them had a spike as good or better as the one observed in Z408 (details)
- The 408 at period 4 transposed or period 102 untransposed has an even more significant (than Z340's) doublet peak. (Source: Jarlve)
Z340
Ngram observations
- Cipher contains 25 repeated bigrams (illustration), 2 repeated trigrams (illustration), and 0 repeated quadgrams.
- In a test of 1,000,000 random shuffles, 110,147 (11%) had 25 or more repeated bigrams (Plot of distribution), and the average number of repeats was 20.
- In a test of 1,000,000 random shuffles, 67,573 (7%) had 2 or more repeated trigrams (Plot of distribution), and the average number of repeats was 0.4.
- In a test of 1,000,000 random shuffles, 7,857 (0.8%) had at least one repeated quadgram (Plot of distribution), and the average number of repeats was 0.008.
- The count of 25 repeating bigrams seems low compared to the average for ciphers with similar IOC generated during experiments (Source)
- 5-gram repeating fragments study
- The IOF trigram repeats in the same columns, and are spaced 8 lines apart, reminiscent of the 8-line height of each of the original 3 parts of the 408 cipher (from Tahoe27). (Illustration) (Illustration)
- TODO: Multidirectional ngram study (including multiple distances, and repeating fragments)
- TODO: Periodicity of repeating fragments study
- Reading the cipher text from left to right and top to bottom, the longest sequence containing no repeated bigrams starts at position 168, and has length 123 (Illustration)
- TODO: periodic ngram / fragment test of individual halves of the 340 (horizontally and vertically), as well as individual "even/odd" transformations.
- Near the end of line 2, K and backwards F appear. Near the beginning of line 19, F and backwards K appear, perfectly mirroring the symbols on line 2. There is an additional symmetry in their placement as corners of the inner box. (Illustration) (by GC)
- The corrected K on line 6 is also next to an F. Does this carry any significance? (Source: druzer)
- The ngram BOUTME appears in both the 1st and 2nd nine-line sections of Z340 after applying the substitution key and lining up the rows to read by columns (Source: rando)
Unigrams
- Index of Coincidence (IoC) of the cipher is 0.0194. This is 4.9% larger than the IoC of Z408.
- IoC divided by cipher length (340) is 0.00005706. This is 26% larger than the IoC per length value for Z408 (Source: Jarlve)
- If you highlight all occurrences of certain symbols, they seem to avoid the middle of the cipher text.
- Kasiski examination of the 340
- Column unigram bias: Certain column combinations seem to be biased towards certain symbols. (Source: Jarlve) (See also: Z13 even/odd bias below)
- Some symbols are unusually clustered or unusually spread apart.
- Compared to shuffles, Z340 has slightly more than expected outliers of unusually distributed symbols.
- Some groups of symbols only appear in pairs of small regions (Source)
- Symbols that exhibit regional bias seem to avoid being involved with perfect cycles (Source: smokie treats)
- Some circles and circle-like symbols seem clustered together. (significance test)
- When counting unique sequences by length, there is a very unusual spike of 26 sequences of length 17. When counts are plotted in a histogram, there is a steep drop off after length 17. The cipher has 17 columns. (Source: jarlve and smokie treats)
- The 20 new symbols in Z340 that aren't in Z408 represent about 80 characters in the cipher. In other words, almost 1/4th of the cipher is represented by symbols not used before (Source: Hubert J. Bernhard)
- I counted 16 symbols that are new to Z340 (about 25% of the size of the cipher alphabet) (illustration)
- I counted 77 occurrences of symbols that are new to Z340 (about 23% of the ciphertext) (illustration)
- The 340 is 68 symbols shorter than the 408. That is a 16.7% decrease. The 340 has 63 distinct symbols, compared to the 408's 54 distinct symbols. This increase is the same percentage, 16.7%. (Source: Mike Cole)
- There may be a spike in period 16, 32, and 48 unigrams, which also involve the symbols in the "pivots" (Source: smokie treats [1]) [2]
- "L" symbols tend to favor a particular side of the cipher text (source: doranchak)
- Somwhat similar effect is seen with Vs and upside down Vs (source: TheMist)
- Regarding the "L"s, the ones in the top half tend to line up in columns (source: Mr. lowe)
- Additional observations of related symbols, by TheMist
- Looking at the triangles, the top of the half has the sequence: Full, empty, full, empty. The bottom half has: empty, full, empty, full.
- The diagonally half-filled squares have the sequence: Right, left, left, left; right, left, left, left.
- The 3 P symbols are each separated by 4 reversed P symbols.
- Symmetry of related symbols (source: Druzer)
- For almost every V, an upside-down V can also been found on the same line. (source: doranchak, TheMist)
- Many of the < and > symbols form a smooth curve pattern. (source: doranchak)
- Symbols in symbol order, for handwriting comparison (source: Fisherman'sFriend)
- There is a symmetry to the "V" and "<" (rotated "V") symbols (source: Zwick808)
- A backwards J symbol appears in the 6th column, just as it does in Z408 and Z32 (source: Jelberg)
- Z340's alphabet consists of 63 unique symbols. Coincidentally, the lengths of Z18, Z13, and Z32 add up to 63. (source: @rogerverreault8682 on YouTube)
Unusual biases in the number of bigram repeats
Top half / bottom half bias
- The lower left of the cipher text seems to contain very few repeated bigrams (see illustration)
- The largest rectangular region that contains no repeats has dimensions 5x10. It covers an area of 50 positions (14.7%) of the cipher.
- Largest rectangular regions were found for 1,000,000 shuffles. 22% of them had ngram-free rectangular areas of size 50 or higher. (details)
- The top half of the cipher text, considered on its own, contains 9 repeated bigrams. However, the bottom half of the cipher text, considered on its own, contains only 1 repeated bigram.
- In 1,000,000 shuffles, only 2.4% of them had halves with a repeated bigram discrepancy as large as the one observed in the 340 (i.e., a difference of at least 8 repeated bigrams between the halves).
- (Distribution of repeated bigram discrepancy among shuffles)
- By contrast, the 408's top half has 17 repeated bigrams and its bottom half has 14.
- If you omit the last column of Z340, the bottom half of the cipher contains zero repeating bigrams. (doranchak)
Even / odd position bias
- The cipher text also shows a bias in repeated ngram counts within even positions and odd positions.
- If you remove all symbols that are in even-numbered positions, there are only 2 repeated bigrams.
- In this case, there are also 0 repeated trigrams.
- If you remove all symbols that are in odd-numbered positions, there are 10 repeated bigrams.
- In this case, there are also 2 repeated trigrams.
- (Illustration)
- The difference in bigram repeats between both cases is 8. During shuffle tests, the difference was 8 or higher in only 2.4% of shuffles. This is the same difference and percentage found for the top half / bottom half bias.
- (Distribution of repeated bigram discrepancy among shuffles)
- In the unmodified 340, there is a "box corner" pattern that repeats. After removing all symbols falling on odd-numbered positions, repeating trigrams appear where the box corner patterns were observed.
- In this illustration, the box corners are highlighted in green on the left. The repeating trigrams are shown on the right, highlighted in purple. Note the repeating sequence "O, half-filled square, C" that is seen in both cases.
- Similar repeating patterns can be also found (illustration)
- 58 unique symbols fall on odd positions (5 symbols missing). 54 symbols fall on even positions (9 symbols missing). The 14 symbols that aren't shared comprise 22% of the 63 total symbols. (Source: daikon)
- If you remove all symbols that are in even-numbered positions, there are only 2 repeated bigrams.
Periodic ngram bias
- Consider the normal way of counting bigrams (one symbol right next to another). Let's call this "period 1" bigrams, because the symbols are one position apart. There are 25 repeating period 1 bigrams. But at other periods, there is a higher count of repeating bigrams. In fact, at period 19, there are 37 repeating bigrams. (Illustration of a small sample of repeating period 19 bigrams)
- Daikon's original observation:
- Jarl's original observation:
- Repeating period 19 bigrams highlighted in the cipher text
- The same, but easier to spot when cipher is written into 19 columns
- A test of 1,000,000 random shuffles suggests a 1 in 216 chance that this is happening by chance (More info)
- If you look at all periods from 2 to 170, 34 of them have 25 or more repeating bigrams. In other words: 20% of other periods have equal or better repeating bigram response than period 1.
- Also, if you flip the ciphertext horizontally (horizontal mirroring), a higher peak occurs at period 15, which produces 41 repeating bigrams. This is consistent with the phenomenon that normal (period 1) bigrams have more repeats when the cipher text is flipped horizontally.
- A test of 1,000,000 random shuffles suggests a 1 in 12821 chance that this is happening by chance (More info)
- A second peak of of 34 repeating bigrams occurs at period 29.
- A third peak of 33 repeating bigrams occurs at period 100.
- Other manipulations that lead to high numbers of bigrams:
- Various row-wise and column-wise offsets and periodic operations lead to between 41 and 45 bigrams. (found by Jarlve and doranchak) (The column offset operation leading to 45 bigrams appears to be significant)
- Column period 2 combined with linear period 18 produces 44 repeating bigrams (doranchak)
- Shift operations combined with periodic untransposition and mirroring leads to 48 bigrams and 8 trigrams. (found by Largo)
- Visualization of bigrams formed via shift operation combined with periodic untransposition (source: Largo)
- "The simplest way to bring the high period 19 results together is columnar odds evens and then raise each column up one space." (Mr. Lowe)
- Plot of periodic bigram counts in normal and mirrored cipher texts (Raw data: Period, # of repeated bigrams in normal 340, # of repeated bigrams in mirrored 340) (Jarlve's plot)
- Plot of periodic trigram counts in normal and mirrored cipher texts (Raw data: Period, # of repeated trigrams in normal 340, # of repeated trigrams in mirrored 340)
- Repeated quadgrams appear only at periods 101 (illustration) and 116 (illustration). They do not appear when considering the mirrored ciphertext.
- A repeated 5-grams appears at period 101 (Illustration)
- Bigram peaks still seem to appear even if you filter out the effects of the symbols that occur 10 or more times (Jarlve's plot - it's the second one there)
- Jarlve's repeating fragment measurements seem to correlate strongly with periods 19 (normal cipher) and 15 (mirrored cipher).
- Inserting a randomized column causes a 40 bigram peak to occur at period 5 (see also)
- TODO: Jarlve's "symbol expansion" test, higher ordered ngrams and fragments
- TODO: how often does a random shuffle show a period that has repeated quadgrams/5grams?
- Visualization tool showing effects of various transposition schemes on bigram/trigram/fragment counts
- Period calculator - A way to visualize the relation of periods to mirrored counterparts, and the effect of untransposition on the interesting patterns (pivots, box corners, and repeating bigrams)
- Z408 has more period 2 bigrams than expected, while Z340 has fewer than expected (Source: Jarlve)
- "Mirror immunity": The number of repeating bigrams is resistant to mirroring operations (source: Largo)
- Jarlve's summary of operations leading to "special bigram peaks" of 41, 44, and 45
- "Herringbone patterns" (Source: smokie treats) [1] [2]
- Periodic ngram peaks resulting from "crossed line" transposition (Source: Largo)
- The use of sequential homophones is a possible explanation for the appearance of periodic outliers (Source: Jarlve)
- A repeating 6-gram can be found when un-transposing certain rows at period 10 (Source: Largo)
Other
- A large block in the 2nd half of the cipher has zero repeating bigrams (Source: doranchak)
Repeated symbols by columns and rows
- The 340 cipher has 9 rows that each contain no repeated symbols (Illustration. Rows are marked in yellow.) In 1,000,000 shuffles, no shuffled cipher text had at least 9 rows with no repeated symbols (plot of distribution) (raw data)
- If you split the cipher in half with a horizontal cut in the middle, the top and bottom halves each start with 3 lines that have no repeated symbols. This symmetry is discussed in Dan Olson's analysis.
- Every column contains at least one repeated symbol.
Homophone cycles
- Tests of cycle significance with shuffle experiments
- Longest-repeating substring search for cycles, compared to shuffles
- Homophone cycles seem to be present but with much weaker regularity than the cycles of Z408.
- Removing row 14 causes significant improvement in perfect cycles (Jarlve)
- Other "irregular" types of cycles are present in Z340 (Raw results and examples)
- When comparing all possible ways that length 6 cycles involving 2 symbols can appear, Z408 and Z340 seem to show very similar behavior. (source: Jarlve)
- Evidence of increasingly random cycles in Z408 and Z340 (source: Jarlve)
- Decreasingly random cycles, for both Z408 and Z340, peak when the cipher is shifted 11 rows downwards (source: Jarlve)
Kasiski Examination
- A Kasiski examination performed on unigrams in Z340 reveals a spike at shift of 78 (Source: Bart Wenmeckers).
- The pivot patterns turn into repeating bigrams at period 39. The number 39 is exactly half of 78. And half of 39 is tantalizingly close to 19, which is the period that produces the peak number of repeating bigrams.
- 26 is a factor of 78 (There are 26 letters in the English alphabet)
- Application of Z408's key to Z340 results in a "plaintext" that still retains a Kasiski examination spike at shift of 78.
- Among 1,000,000 random shuffles, only 0.28% of them had a spike as good or better as the one observed in Z340 (details)
- For shift values of 2 through 6, the number of repeats is unusually low (1 or 2). (source)
- Visualization of peak at shift 78 by viewing as doubles in untransposed period 78 (with pivots highlighted)
- The doubles are easier to see when Z340 is transcribed to width 26
- When calculating column IoC at different column widths, spikes are observed at widths 39 and 78. (Source: Bart Wenmeckers)
- When looking at normalized means of columnar IoC, resonances at multiples of 5 are observed. . (Source: doranchak)
- The use of sequential homophones is a possible explanation for the spike in doublets at offset 78 (Source: Jarlve)
The "Pivots"
- The 340 contains a pair of intersecting repeating trigrams. We refer to each repeating trigram as a "pivot". Illustration and analysis (Source: bentley, 2010, and Smithy)
- These anomalies both occur 4 columns in from the side and one column from the center. (Source: bentley, 2010)
- The pivot patterns become repeating bigrams if you rewrite the cipher text at period 39.
- When calculating column IoC at different column widths, spikes are observed at widths 39 and 78 (see Kasiski examination section above)
- When numbering the cipher text from 1 to 340, the intersections of the pivot patterns fall on positions 195 and 234, which are 39 positions apart. Interestingly, 195 and 234 are both evenly divisible by 39. (source)
- Similarly, the pivot patterns become repeating bigrams if you mirror the cipher text horizontally and rewrite it at period 29.
- Period 29 is the 2nd highest periodic bigram peak for the mirrored 340 (see the Periodic ngram bias section above)
- In an experiment, the 340 was randomly shuffled over 41 million times. A pair of pivots that point in the same direction was only observed in about 1 in 237,000 shuffles.
- In this study the 340 was shuffled and the number of repeating bigrams was fixed at a set number. Transposition was performed and pivot pairs were counted. The results show that higher bigram counts cause pivot pairs to be created more often, but they are still rare.
- The reversed B symbols occurs only three times and cluster around the pivots. (Source: Largo)
- Diagonal lines drawn through the forward slash symbols "boxes in" the pivots. (Source: Biz)
- Other repeating pairs of symbols near the pivots are suggestive of possible "incomplete" pivots. (Source: Largo)
- The plus and filled in circle symbols repeat in the same positions relative to each pivot. (Source: Mr lowe)
- In light of the known solution and transposition steps, the pair of pivots vaguely resembles arrowheads suggestive of the reading direction.
- 9 out of 14 of the plaintext letters forming the pivots involve the letters A, E, or N. In both the 340 and 408 keys, the backwards L symbol decodes to A, the N symbol decodes to E, and the D symbol decodes to N. Those are the only symbols that decode to the same letter. Also, Z13 begins with the same three letters: AEN. (Source: Sam Fisher)
- "BELLI" (as in Melvin Belli) appears in reverse in the 2nd to last line of the raw plaintext, before word reversals are applied. (Source: Shawn)
- The name "BEN REECE" appears in a cross formation in the raw plaintext. (Source: Shawn-z)
- "If you have a tool or device for reading the message or key that has holes in it or something you can wrap around a device that is the key with diagonal holes. If the holes are diagonal, they will meet at the corners and the device will be weak where the corners meet. If you go down and over two spaces, there is plenty of material left between the holes at the corners and so the device can be solid." (Source: Myron Walker, via YouTube comment on LCZ episode 6)
- "First plain word of the first section HER, First line of second section LIFE IS. Could the cipher have been designed to leave these in the plain to indicate that the cipher is divided into two section, it would be interesting to see if HER or LIFE IS was used to make the key" (Source: Myron Walker, via YouTube comment on LCZ episode 6)
- "I think the last two lines were there to help find the key. That's why they were not transposed" (Source: Myron Walker, via YouTube comment on LCZ episode 9)
- Note: A solver could have focused on just those two lines, but the multiplicity is too high (88.2%). So there probably aren't enough repeats to find a unique plaintext.
- In the last 4 lines of the cipher, a 6-symbol section decodes to "HARDEN" (reference to the Hardens) when the symbols are individually reversed. (Source: rando)
- The untransposed plaintext has a 13-character section beginning with A and ending with M. Z13 also begins with A and ends with W. (Source: cragle)
- If you count the letters in "life is" and the shifted letters "ratenyrnosrvs", they add up to 19 (the period required to transpose the plaintext) (Source: @timpsensky5181 on YouTube)
Other observations
- Application of 408's key to the 340:
- Applying the 408's key to the 340 produces this plaintext.
- The words "NET NULL" appear
- Per FBI, applying the 408's key yields plaintext frequencies similar to expected English plaintext (source: FBI case files)
- Some symbols in the 340 were not in the 408's alphabet (Image)
- The paper the cipher is written on contains several Fifth Avenue watermarks (here's glurk's animation to help you spot where they appear).
- The first 3 symbols of the 340 do not reappear soon. It starts with "HER", and H only appears 3 other times, E only appears 2 other times. (From Duman)
- In the third column, the 3 occurrences of the "R" symbol are evenly spaced, each separated by four rows. (From Wrench)
- The author of the cipher does not use the forward-facing letter Q as a cipher symbol, but uses a backwards-facing Q instead. Similarly, he does not use the forward-facing letter C as a cipher symbol in the 408-character cipher, but uses a backwards-facing C instead. Why doesn't he use up all the normal alphabetic symbols before resorting to additional symbols and variations? (one possible explanation)
- The first repeated symbol occurs at the 19th position. Thus the first 18 symbols contain no repeats. Coincidentally, the last 18 symbols of the 408 cipher do not form a legible solution. (From traveller1st)
- The most frequently occurring symbol, +, occurs 24 times. Only once does it fall on a prime-numbered position in the cipher text (counting from 1 to 340), against expectations. Also both occurrences of the X symbol fall on prime positions against expectations. (More detail) (From Dan Johnson) (TODO: Prime phobia distribution study for all symbols)
- The second most frequently occurring symbol, B, occurs 12 times. Only once does it fall on a prime-numbered position in the cipher text (counting from 1 to 340), against expectations. (More detail) (From Dan Johnson)
- The upper loop of the "B" symbol on line 19 column 9 is larger than the lower loop, making the symbol look disproportional and distinct from the other "B" symbols. (From Doc. Doc also speculates the symbol was original a "P" and the author corrected it by adding the bottom loop.)
- The last occurrence of the "+" symbol is wider than the others. (From Doc. Doc speculates that the author "hesitated" on this symbol.)
- Cipher symbols seem to get larger as the cipher goes on. Row 20 seems larger than Row 1. (From Doc. Doc speculates the author wrote the cipher from top to bottom, and was tiring.)
- The backwards D at the end of the first line appears to have a dot in it (Source: comment from "The McNX")
- The symbols that represent "R" in the 408 are
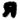 and
and 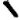 . Both symbols are missing from the 340 cipher. (Source: Wier)
. Both symbols are missing from the 340 cipher. (Source: Wier) - The symbol '+' is frequently adjacent (in all directions, not just left/right) to the symbol 'R'. (Source: http://www.zodiackillersite.com/viewtopic.php?p=39791#p39791). 'B' is the 2nd most common symbol in the cipher (12 appearances), but for some reason it is adjacent to only one of the 24 '+' symbols.
- The average of the position numbers for all occurrences of the '+' symbol is 171, which is only one position from the midpoint of the cipher. This suggests the + symbols are very uniformly distributed throughout the ciphertext. (Source: Jarlve)
- The '+' symbol does not seem to cycle well with other symbols. (Source: Jarlve)
- A tiny 'R' is written at the bottom right corner of the page. Similarly, information is written at the bottom right corner of a section of the 408, and the bottom right corner of the letter containing the map code.
- Cycles of length 2 are biased towards odd-numbered positions in the cipher text
- The 340 has 9 rows that each have no repeated symbols. By comparison, the 408 has 6. Moreover, in the 340, there are two triplets of rows that show symmetry about the vertical midpoint of the cipher text. See [1]. (Image of row repeat comparisons)
- A forward-K appears to be scratched out, and corrected with a backwards K symbol. (Image)
- The backwards K symbol is written with the slanted segments joining perfectly in the middle. But the forwards K symbol is written with the slanted segments offset from each other. (Source: vtschoir)
- W symbols are flared and M symbols are not. (Source: vtschoir)
- "I noticed that as I progressed down the grid, I was able to mostly predict some subtle features. By and large, if a symbol was reversible such as '<' or '>' or '^' or 'v' you would regularly encounter more than 1 variation of the symbol on the same line or collumn, but very rarely see straight up duplicates. The '+' symbol is, by a massive margin, the most common symbol to be seen in duplicate. As symbols which used a circle in them were used, I was more or less able to say 'I bet the next circle isn't the same as the one already on this line or collumn.' So I'd see an empty one, then a split one, then a full one, then a half shaded one... Almost as if differentiating them was an after-thought, to ensure everyone had a harder time trying to decipher it. (Source: vtschoir)
- From Scott Akin: All occurrences of the "H" symbol are involved with this observation: Consider the rectangular regions formed by the corners highlighted in this illustration. Each region is exactly 80 characters in size (4x20 and 5x16), and there is symmetry to the corner symbols.
- Largo's test finds that this often occurs by chance, even with random text.
- From "Haley25": Zodiac's "bus bomb letter" contains a section he highlighted which, when punctuation (except for "and" signs and the hyphen) and spaces are removed, contains exactly 340 letters. (source) (illustration)
- From Shawn: BTK's word search puzzle has exactly 340 letters and numbers in it.
- Line 11 is suggestive of the phrase "U R TO DIE BY" (Illustration) (Source: bentley)
- Appearance of anagrams of the word "FOLD" (Source: forbisgaryg) (Illustration)
- Clusters of rotationally-related symbols (Illustration) (See also: "box corners" discussed above.)
- Symbols arranged by appearance
- The "dripping pen" card that accompanied the cipher contains a series of months written by Zodiac: "Des July Aug Sept Oct". This sequence is exactly 17 letters long (not including spaces), which matches the width of the Z340, Z408 and Z32 ciphers.
- Spelling the months in full without spaces, as DECEMBERJULYAUGUSTSEPTEMBEROCTOBER, is exactly 34 letters long (double 17). (source: Marclean)
- The dot symbols are placed higher than the midpoint of the row of symbols in which they appear. (Source: Jarlve)
- Row spacing appears more regular than column spacing, suggesting the cipher was written out by rows. (Source: Jarlve)
- There is extra spacing between rows 12 and 13. The smallest gap, however, appears to be between rows 13 and 14, as if to make up for the extra spacing taken between rows 12 and 13. (Source: Jarlve and doranchak)
- Horizontal mirror of the cipher produces some coincidences with the Halloween card (Source: jaydeezodiachunter)
- The symbols line up very well with each other, and fit within a perfectly rendered grid, suggesting the cipher author may have used such a grid to draft the cipher text (Illustration 1) (Illustration 2) (Source: Sam Blake)
- Some symbols are smudged, suggestive of the cipher author's hand passing over the fresh ink of written symbols (Illustration by Sam Blake)
- Similar groupings of related symbols by quadrant (Source: Cragle)
- 340 is an "arithmetic number" for which the average of its divisors (1, 2, 4, 5, 10, 17, 20, 34, 68, 85, 170, 340) is exactly 63, matching the cipher's alphabet size. (Source: G. L. Honaker, Jr)
- The length of Z408 with the last 18 symbols of gibberish or filler removed is 390, which is also an "arithmetic number" whose divisors have an average of exactly 63. (Source: doranchak)
- American astronomer Vesto Melvin Slipher, noted for his analysis of Zodiacal Light, died on the day Z340 was mailed to the San Francisco Chronicle. (Source: G. L. Honaker, Jr)
- Comparison of Z408 key with Z340 key via shifts (Source: upsampled)
- A sequence of symbols in the upper left corner of the cipher resembles the word "cipher".
- The accompanying card has a section with dates, presumably denoting Zodiac's crimes. Flipping it over makes it resemble the phrase "L = codes" (Source: UK-Chris on Discord)
Z408 and Z340
- "The 408 and 340 ciphers fit exactly into two standard-size pages ruled into half-inch squares. The 408 will use one page plus one inch from another page. The second page will then fit the 340 exactly." (from Jem) (Open question: Is the 340 a continuation of the 408?)
- "An 8 1/2 X 11 inch paper divided into 1/2" squares yields 17X22 or 374 separate squares. Two pages together: 374 X 2= 748. The two ciphers together? 748 symbols." (from entropy)
- Illustration showing how the 408 and 340 fit exactly on two sheets of 0.5" ruled grid paper
- The 408's cipher alphabet is missing the cipher symbol C. The 340's cipher alphabet is missing the cipher symbol Q. It is strange that in both ciphers, Zodiac left out one letter from the cipher alphabet. He bothered to create new shapes and rotated letters, but still left out a "normal" letter in each cipher.
- Unverified: When the 340 and 408 ciphers are considered together, there is a total of 341 alphabetic symbols, and 407 non-alphabetic symbols. Both counts only differ by one with the respective cipher lengths. (Source: Marclean)
- Z408 and Z340 each have an alphabet size that is divisible by 9: "9x7 = 63 Z340, 9x6 = 54 Z408. Just for inclusion 7 symbols were dropped from Z408 and 16 were added for a net gain of 9 in Z340." (Source: BartW)
- When written vertically, some symbols repeat in a pattern similar to the period-19 reading order used to decrypt the Z340 (Source: Marclean)
Z13
- Symbols on even positions do not repeat. Symbols on odd positions do (N and circled 8). (Source: daikon)
- The cipher contains three symbols that look like circled 8's. Coincidentally, there are 8 "normal" symbols (excluding the upside down T). (Source: Ed Pittman)
- There are 13 symbols, with A as the first and M as the last. This fits with the first half of the alphabet; there are 13 letters, A is the first, M is the last. AbcdefghijklM (Source: egg)
- The order of alphabet and non-alphabet characters is mirrored (or palindromic): (3-2-1-1-1-2-3): aen??k?m??nam (Source: egg)
- N is the third letter from the start and third from the end. (Source: egg)
- It is possible to linearly sequence part of the alphabet mirrored around the central ciphered character: nmlklmn (Source: egg) (Visualization)
- Letters from the word "NAME" appear in the cipher text. The cleartext prior to the cipher says "My name is _____".
- The "circled 8" or "taurus" symbols are in symmetrical positions with respect to the center of the cipher text.
- "N" and "M" symbols appear in an orderly sequence: N, M, N and M. (Illustration)
- The "circled 8" or "taurus" symbols do not appear in Zodiac's other 3 ciphers. The upside down T also appears in Z32.
- The word "WANT" appears when the cipher is flipped vertically. (Illustration)
- 3 symbols line up with a section of Z340. (Source: traveller1st) (original broken link)
- The "E"s in the last 18 letters of Z408's plaintext line up with the 3 circled 8 symbols in Z13. (Illustration)
- The cipher text resembles Greek inscription "anetheke" which appears on ancient Greek temples and artifacts. (Source: Tom Voigt) (More examples)
- Decrypting the first 6 symbols of Z13 with Z408's and Z340's key produces plaintext letters that are clustered on a standard keyboard layout (Source: marclean)
- If you skip 8 positions from each 8-ball symbol (including wrap around), it spells ME⌖ (Source: https://twitter.com/whatever23978)
- The "p.s." section in the bus bomb letter, when reversed, contains "AEN" and "NAM" which are also found in Z13. "K" and "M" also appear in the correct order (respective to Z13). (source: rando, Shaqmeister)
- The October 5th 1970 card has 13 holes punched in it, reminiscent of the 13 symbols in Z13.
Z13 and Z32
- Z13 begins with 3 symbols followed by a crosshairs symbol. Z32 ends with a crosshairs symbol followed by 3 symbols. (Source: Mike Cole) (Illustration)
- The line lengths of Z32 and Z13 are 17, 15, 13. (Source: Martin Jeppesen)